Angle relationships are the hidden language of geometry that help us understand the world around us. Imagine walking into a room with perfect symmetry or observing the angles in a bridge that hold everything together. Geometry isn’t just shapes; it’s a fascinating web of connections, and understanding angle relationships is the key to unlocking this intricate puzzle. Whether you're a student trying to ace your geometry exam or a curious mind exploring the beauty of math, this guide will take you on an exciting journey through the world of angles.
Math might feel overwhelming sometimes, but when you break it down into bite-sized pieces, it becomes a lot easier. Angle relationships are one of those concepts that can seem tricky at first glance, but once you get the hang of it, you'll see how logical and beautiful they really are. This guide will walk you through everything you need to know, from the basics to the more advanced stuff.
So, grab your notebook and a cup of coffee because we're diving deep into the world of angles. By the end of this article, you’ll not only understand what angle relationships are but also how they apply to real-world scenarios. Let’s get started!
- Cassandra Peterson Bra Size Unveiling The Iconic Elviras Glamorous Secrets
- Where To Watch The Grammy Red Carpet Your Ultimate Guide For 2024
What Are Angle Relationships Anyway?
Let’s start with the basics. Angle relationships refer to how different angles interact and relate to each other. Think of it like a family tree for angles. Just like people in a family have relationships, angles also have their own connections. These relationships are defined by their position, measurement, and interaction with other angles.
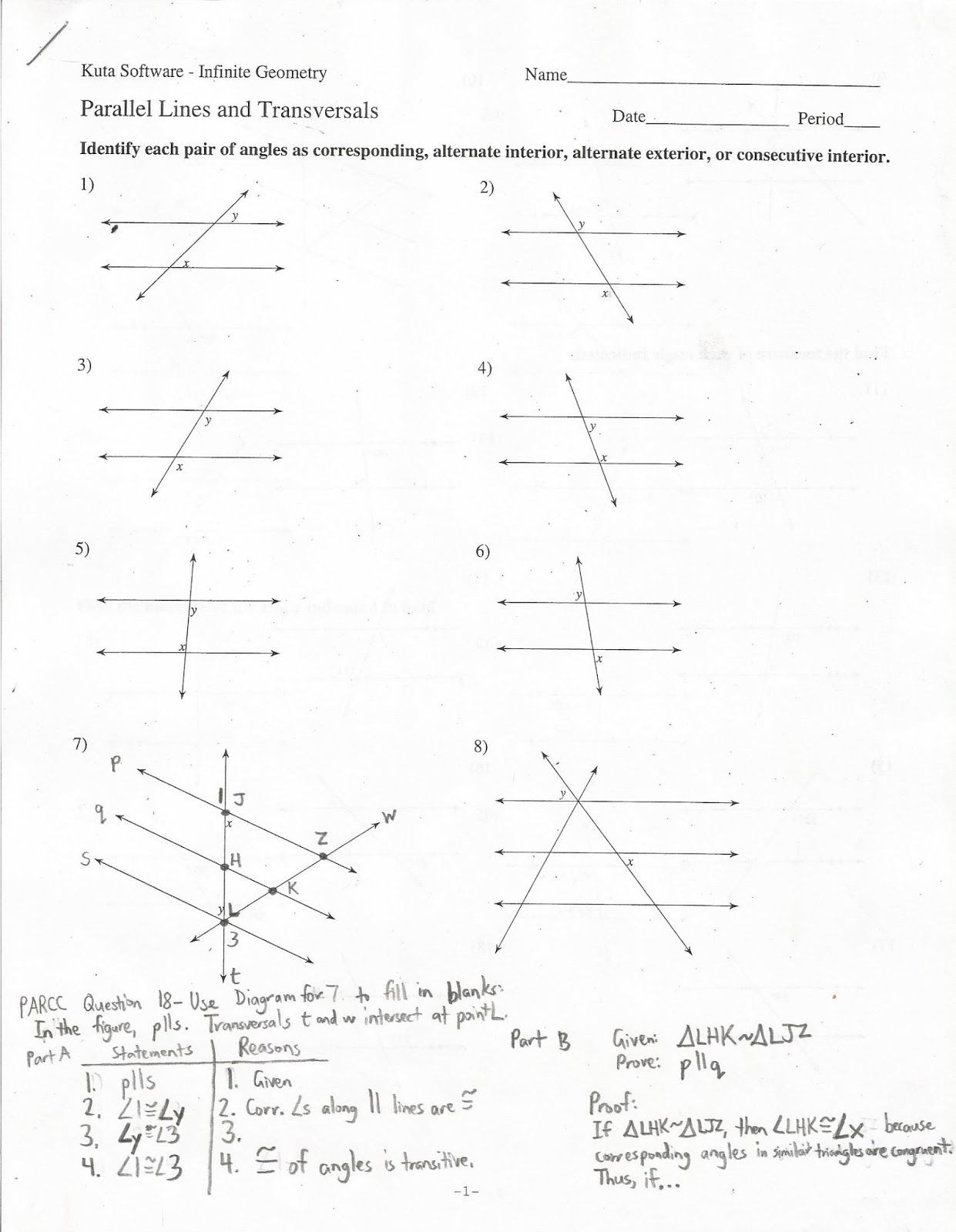
Some common types of angle relationships include complementary, supplementary, adjacent, vertical, and linear pairs. Each of these relationships has its own set of rules and characteristics. For example, complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. Adjacent angles share a common vertex and side, while vertical angles are opposite each other when two lines intersect.
Understanding these relationships is crucial because they form the foundation for more complex geometric concepts. It’s like learning the alphabet before you start reading books. Once you grasp the basics, you can move on to more advanced topics like trigonometry and calculus.
- Harry Potter Reboot The Magic Returns In A Whole New Way
- Nicole Blue The Rising Star Whorsquos Taking The World By Storm
Types of Angle Relationships
Complementary Angles
Complementary angles are like best friends who always stick together. They add up to exactly 90 degrees. For instance, if one angle measures 30 degrees, the complementary angle will measure 60 degrees. These angles are often found in right triangles, where one angle is 90 degrees and the other two angles are complementary.
Supplementary Angles
Supplementary angles, on the other hand, are like a duo that adds up to 180 degrees. Think of them as a straight line. If one angle measures 120 degrees, the supplementary angle will measure 60 degrees. These angles are commonly seen in parallel lines and transversals.
Adjacent Angles
Adjacent angles are like neighbors who share a common boundary. They share a common vertex and side but do not overlap. For example, if you have a straight line with a point dividing it into two angles, those two angles are adjacent.
Vertical Angles
Vertical angles are the opposite angles formed when two lines intersect. They are always equal in measure. For instance, if one vertical angle measures 45 degrees, the opposite angle will also measure 45 degrees. These angles are often used in proofs and problem-solving in geometry.
Linear Pairs
Linear pairs are adjacent angles that form a straight line. They are supplementary, meaning they add up to 180 degrees. For example, if one angle in a linear pair measures 110 degrees, the other angle will measure 70 degrees.
Why Are Angle Relationships Important?
Angle relationships might seem like abstract concepts, but they have real-world applications. Architects use angle relationships to design buildings that are structurally sound. Engineers rely on these relationships to create bridges and roads that can withstand various forces. Even artists use angles to create visually appealing compositions.
In everyday life, you might not realize it, but you encounter angle relationships all the time. When you park your car, you’re using angles to determine the best position. When you throw a ball, you’re calculating angles to make sure it lands where you want it to. Understanding angle relationships can help you make sense of the world around you.
How to Identify Angle Relationships
Using Diagrams
One of the easiest ways to identify angle relationships is by using diagrams. Visual aids can help you see how angles interact with each other. For example, if you draw two intersecting lines, you can easily identify the vertical angles and linear pairs.
Applying the Rules
Each type of angle relationship has its own set of rules. For instance, if you know that two angles are complementary, you can subtract one angle from 90 degrees to find the other. Similarly, if you know that two angles are supplementary, you can subtract one angle from 180 degrees to find the other.
Using Algebra
Angle relationships can also be expressed algebraically. For example, if you have two complementary angles, you can set up an equation like x + y = 90. Solving for one variable will give you the measure of the other angle.
Real-World Applications of Angle Relationships
Architecture and Construction
Architects use angle relationships to ensure that buildings are structurally sound. They calculate angles to determine the best placement for beams and supports. Without a proper understanding of angle relationships, buildings could collapse or become unstable.
Engineering
Engineers rely on angle relationships to design bridges, roads, and other infrastructure. They calculate angles to ensure that structures can withstand various forces, such as wind and weight. For example, the angles in a suspension bridge are carefully calculated to distribute weight evenly.
Art and Design
Artists use angle relationships to create visually appealing compositions. They use angles to create balance and symmetry in their work. Even something as simple as arranging furniture in a room involves understanding angles to create a harmonious space.
Common Mistakes When Working with Angle Relationships
Even the best mathematicians make mistakes sometimes. One common mistake is confusing complementary and supplementary angles. Remember, complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. Another mistake is forgetting that vertical angles are always equal. Lastly, some people forget that adjacent angles share a common vertex and side.
Advanced Concepts in Angle Relationships
Transversals and Parallel Lines
When a transversal intersects two parallel lines, several angle relationships are formed. These include corresponding angles, alternate interior angles, and alternate exterior angles. Each of these relationships has its own set of rules and characteristics. Understanding these relationships is crucial for solving more complex geometry problems.
Angles in Polygons
Angle relationships also apply to polygons. The sum of the interior angles of a polygon can be calculated using the formula (n-2) × 180, where n is the number of sides. For example, a triangle has three sides, so the sum of its interior angles is (3-2) × 180 = 180 degrees.
Trigonometry
Trigonometry builds on the foundation of angle relationships. It involves the study of triangles and the relationships between their sides and angles. Trigonometric functions like sine, cosine, and tangent are used to solve problems involving angles and distances.
Tools and Resources for Learning Angle Relationships
There are plenty of tools and resources available to help you learn angle relationships. Online geometry calculators can help you solve problems quickly and accurately. Interactive geometry software allows you to visualize angle relationships and experiment with different scenarios. Additionally, there are countless tutorials and videos available on platforms like YouTube and Khan Academy.
Conclusion
Angle relationships might seem like a small part of geometry, but they play a big role in our understanding of the world. From architecture to art, these relationships are everywhere. By mastering the basics and exploring more advanced concepts, you can unlock the secrets of geometry and apply them to real-world situations.
So, what’s next? Start practicing with diagrams and equations. Challenge yourself with real-world problems. And don’t forget to have fun! Math is more than just numbers; it’s a way of thinking and understanding the world around us. Share this article with your friends and family, and let’s spread the love for geometry together!
Table of Contents
- What Are Angle Relationships Anyway?
- Types of Angle Relationships
- Why Are Angle Relationships Important?
- How to Identify Angle Relationships
- Real-World Applications of Angle Relationships
- Common Mistakes When Working with Angle Relationships
- Advanced Concepts in Angle Relationships
- Tools and Resources for Learning Angle Relationships
- Conclusion
- Nathan Thompson Wife Unveiling The Life And Love Of A Rising Star
- Elementary Cast Season 4 A Deep Dive Into The Characters And Their Journey